⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀✦ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀✦ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀✦ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀✦ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀✦ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀✦ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀
⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀✦ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀✦ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀✦ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀✦ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀ ⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀✦ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀ ⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀✦ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀✦ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀ ⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀✦ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀✦ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀✦ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀ ⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀✦ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀ ⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ✦⠀ ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ゚ . . ✦ , ✦ . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀⠀ * . . . ⠀ ✦ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀✦ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀ ⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ⠀ , * ✦ ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . ✦ . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀✦ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀ ⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ✦ ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ゚ . ✦ . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ✦ ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ✦ ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ゚ . . ✦ ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . ✦⠀ . *⠀ ⠀ ⠀✦⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ゚ . ✦ . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ✦⠀ ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀✦ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ✦ ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ✦ ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀✦ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ゚ . . ✦ , ✦ . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀✦⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦ ⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ゚ . . ✦ , ✦ . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦ ⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀ ✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ✦ ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀ ✦ ˚ * .⠀ . . ✦⠀ , .✦ ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀✦ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . ⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀⠀⠀. . ⠀⠀⠀⠀⠀✦⠀⠀⠀⠀⠀⠀⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀✦ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀⠀⠀. ✦ . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀ ⠀⠀⠀. . ゚ . ✦⠀ . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀⠀ * . . . ⠀ . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, * ⠀. . ⠀✦ ˚ * .⠀ . . ✦⠀ , . ⠀⠀⠀⠀⠀⠀. ⠀⠀⠀✦ ⠀ ⠀ ⠀⠀⠀⠀⠀* ⠀⠀⠀. . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀✦⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ ⠀ ⠀⠀⠀⠀⠀⠀. . ゚ . . ✦ , . ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ * . . . ✦⠀ , * ⠀ ⠀ , ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀. ⠀ ⠀. ˚ ⠀ ⠀ , . . *⠀ ⠀ ⠀✦⠀ * . . . . ˚ ゚ . .⠀ ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀, ✦⠀
. ' . + . + * . ' + . . . + . ' . ' ' * . ' * . ' + * . ' ' + . + ' ' + + + + * ' + * ' ' ' * + * . ' * ' ' . + . ' . ' * . ' ' . . + . . ' . ' . . ' ' . * ' + * + ' . ' ' . + * + . * ' . . + ' ' + * . + ' . . ' ' ' * ' ' . . . ' . ' . + + * . . . ' . + . ' + ' + + ' * + * + . . . + ' ' + ' . ' ' . ' ' ' ' ' . + + ' . ' . . + . . + . . . . ' . + * * . * ' . . . ' . + ' * . + + + . . * * . ' ' . + ' ' . * . . ' ' . * . . * . + + ' . . . + . + . . + + ' . ' ' ' ' + . * ' . . . . . . ' . ' + + * ' ' * . . . ' ' ' * ' . ' ' ' ' + . ' + ' . ' . + . . . ' ' ' ' . ' . ' . . + + . * ' + + ' ' ' ' . . . ' . + . + * . ' + . . . + . ' . ' ' * . ' * . ' + * . ' ' + . + ' ' + + + + * ' + * ' ' ' * + * . ' * ' ' . + . ' . ' * . ' ' . . + . . ' . ' . . ' ' . * ' + * + ' . ' ' . + * + . * ' . . + ' ' + * . + ' . . ' ' ' * ' ' . . . ' . ' . + + * . . . ' . + . ' + ' + + ' * + * + . . . + ' ' + ' . ' ' . ' ' ' ' ' . + + ' . ' . . + . . + . . . . ' . + * * . * ' . . . ' . + ' * . + + + . . * * . ' ' . + ' ' . * . . ' ' . * . . * . + + ' . . . + . + . . + + ' . ' ' ' ' + . * ' . . . . . . ' . ' + + * ' ' * . . . ' ' ' * ' . ' ' ' ' + . ' + ' . ' . + . . . ' ' ' ' . ' . ' . . + + . * ' + + ' ' ' ' . .
. ' . + . + * . ' + . . . + . ' . ' ' * . ' * . ' + * . ' ' + . + ' ' + + + + * ' + * ' ' ' * + * . ' * ' ' . + . ' . ' * . ' ' . . + . . ' . ' . . ' ' . * ' + * + ' . ' ' . + * + . * ' . . + ' ' + * . + ' . . ' ' ' * ' ' . . . ' . ' . + + * . . . ' . + . ' + ' + + ' * + * + . . . + ' ' + ' . ' ' . ' ' ' ' ' . + + ' . ' . . + . . + . . . . ' . + * * . * ' . . . ' . + ' * . + + + . . * * . ' ' . + ' ' . * . . ' ' . * . . * . + + ' . . . + . + . . + + ' . ' ' ' ' + . * ' . . . . . . ' . ' + + * ' ' * . . . ' ' ' * ' . ' ' ' ' + . ' + ' . ' . + . . . ' ' ' ' . ' . ' . . + + . * ' + + ' ' ' ' . . . ' . + . + * . ' + . . . + . ' . ' ' * . ' * . ' + * . ' ' + . + ' ' + + + + * ' + * ' ' ' * + * . ' * ' ' . + . ' . ' * . ' ' . . + . . ' . ' . . ' ' . * ' + * + ' . ' ' . + * + . * ' . . + ' ' + * . + ' . . ' ' ' * ' ' . . . ' . ' . + + * . . . ' . + . ' + ' + + ' * + * + . . . + ' ' + ' . ' ' . ' ' ' ' ' . + + ' . ' . . + . . + . . . . ' . + * * . * ' . . . ' . + ' * . + + + . . * * . ' ' . + ' ' . * . . ' ' . * . . * . + + ' . . . + . + . . + + ' . ' ' ' ' + . * ' . . . . . . ' . ' + + * ' ' * . . . ' ' ' * ' . ' ' ' ' + . ' + ' . ' . + . . . ' ' ' ' . ' . ' . . + + . * ' + + ' ' ' ' . . . ' . + . + * . ' + . . . + . ' . ' ' * . ' * . ' + * . ' ' + . + ' ' + + + + * ' + * ' ' ' * + * . ' * ' ' . + . ' . ' * . ' ' . . + . . ' . ' . . ' ' . * ' + * + ' . ' ' . + * + . * ' . . + ' ' + * . + ' . . ' ' ' * ' ' . . . ' . ' . + + * . . . ' . + . ' + ' + + ' * + * + . . . + ' ' + ' . ' ' . ' ' ' ' ' . + + ' . ' . . + . . + . . . . ' . + * * . * ' . . . ' . + ' * . + + + . . * * . ' ' . + ' ' . * . . ' ' . * . . * . + + ' . . . + . + . . + + ' . ' ' ' ' + . * ' . . . . . . ' . ' + + * ' ' * . . . ' ' ' * ' . ' ' ' ' + . ' + ' . ' . + . . . ' ' ' ' . ' . ' . . + + . * ' + + ' ' ' ' . . . ' . + . + * . ' + . . . + . ' . ' ' * . ' * . ' + * . ' ' + . + ' ' + + + + * ' + * ' ' ' * + * . ' * ' ' . + . ' . ' * . ' ' . . + . . ' . ' . . ' ' . * ' + * + ' . ' ' . + * + . * ' . . + ' ' + * . + ' . . ' ' ' * ' ' . . . ' . ' . + + * . . . ' . + . ' + ' + + ' * + * + . . . + ' ' + ' . ' ' . ' ' ' ' ' . + + ' . ' . . + . . + . . . . ' . + * * . * ' . . . ' . + ' * . + + + . . * * . ' ' . + ' ' . * . . ' ' . * . . * . + + ' . . . + . + . . + + ' . ' ' ' ' + . * ' . . . . . . ' . ' + + * ' ' * . . . ' ' ' * ' . ' ' ' ' + . ' + ' . ' . + . . . ' ' ' ' . ' . ' . . + + . * ' + + ' ' ' ' . . . ' . + . + * . ' + . . . + . ' . ' ' * . ' * . ' + * . ' ' + . + ' ' + + + + * ' + * ' ' ' * + * . ' * ' ' . + . ' . ' * . ' ' . . + . . ' . ' . . ' ' . * ' + * + ' . ' ' . + * + . * ' . . + ' ' + * . + ' . . ' ' ' * ' ' . . . ' . ' . + + * . . . ' . + . ' + ' + + ' * + * + . . . + ' ' + ' . ' ' . ' ' ' ' ' . + + ' . ' . . + . . + . . . . ' . + * * . * ' . . . ' . + ' * . + + + . . * * . ' ' . + ' ' . * . . ' ' . * . . * . + + ' . . . + . + . . + + ' . ' ' ' ' + . * ' . . . . . . ' . ' + + * ' ' * . . . ' ' ' * ' . ' ' ' ' + . ' + ' . ' . + . . . ' ' ' ' . ' . ' . . + + . * ' + + ' ' ' ' . . . ' . + . + * . ' + . . . + . ' . ' ' * . ' * . ' + * . ' ' + . + ' ' + + + + * ' + * ' ' ' * + * . ' * ' ' . + . ' . ' * . ' ' . . + . . ' . ' . . ' ' . * ' + * + ' . ' ' . + * + . * ' . . + ' ' + * . + ' . . ' ' ' * ' ' . . . ' . ' . + + * . . . ' . + . ' + ' + + ' * + * + . . . + ' ' + ' . ' ' . ' ' ' ' ' . + + ' . ' . . + . . + . . . . ' . + * * . * ' . . . ' . + ' * . + + + . . * * . ' ' . + ' ' . * . . ' ' . * . . * . + + ' . . . + . + . . + + ' . ' ' ' ' + . * ' . . . . . . ' . ' + + * ' ' * . . . ' ' ' * ' . ' ' ' ' + . ' + ' . ' . + . . . ' ' ' ' . ' . ' . . + + . * ' + + ' ' ' ' . . . ' . + . + * . ' + . . . + . ' . ' ' * . ' * . ' + * . ' ' + . + ' ' + + + + * ' + * ' ' ' * + * . ' * ' ' . + . ' . ' * . ' ' . . + . . ' . ' . . ' ' . * ' + * + ' . ' ' . + * + . * ' . . + ' ' + * . + ' . . ' ' ' * ' ' . . . ' . ' . + + * . . . ' . + . ' + ' + + ' * + * + . . . + ' ' + ' . ' ' . ' ' ' ' ' . + + ' . ' . . + . . + . . . . ' . + * * . * ' . . . ' . + ' * . + + + . . * * . ' ' . + ' ' . * . . ' ' . * . . * . + + ' . . . + . + . . + + ' . ' ' ' ' + . * ' . . . . . . ' . ' + + * ' ' * . . . ' ' ' * ' . ' ' ' ' + . ' + ' . ' . + . . . ' ' ' ' . ' . ' . . + + . * ' + + ' ' ' ' . . . ' . + . + * . ' + . . . + . ' . ' ' * . ' * . ' + * . ' ' + . + ' ' + + + + * ' + * ' ' ' * + * . ' * ' ' . + . ' . ' * . ' ' . . + . . ' . ' . . ' ' . * ' + * + ' . ' ' . + * + . * ' . . + ' ' + * . + ' . . ' ' ' * ' ' . . . ' . ' . + + * . . . ' . + . ' + ' + + ' * + * + . . . + ' ' + ' . ' ' . ' ' ' ' ' . + + ' . ' . . + . . + . . . . ' . + * * . * ' . . . ' . + ' * . + + + . . * * . ' ' . + ' ' . * . . ' ' . * . . * . + + ' . . . + . + . . + + ' . ' ' ' ' + . * ' . . . . . . ' . ' + + * ' ' * . . . ' ' ' * ' . ' ' ' ' + . ' + ' . ' . + . . . ' ' ' ' . ' . ' . . + + . * ' + + ' ' ' ' . .
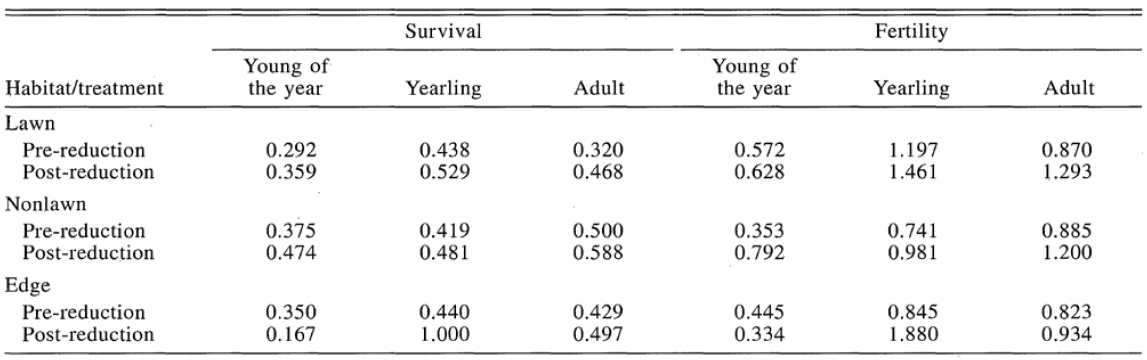
Figure 1: Survival and fertility data for 3 age classes of the Uinta Ground Squirrel population
In the 1960s and 1970s, scientists performed an experimental reduction in the population density of Uinta Ground Squirrels in three types of habitats in Utah. These researchers consolidated six years of data collected before and after the population reduction, into a single life table containing the survival and fertility rates of female squirrels across three age classes that constitute the squirrel population.
In the context of this experiment, the survival rate is a number between 0 and 1 that refers to the probability than an individual within an age class will survive through the current time interval. The fertility rate refers to the average number of newborn females produced by one female in a particular age class that survive through the time interval in which they were born.
The study categorized the squirrel population into three age classes: young, yearlings, and adults. “Young” refers to squirrels less than 1 year old, “yearlings” refers to squirrels between 1 and 2 years of age, and “adults” are squirrels older than 2 years. Consequently, each time interval, denoted as t, represents a one-year interval. For example, t would be the current year, and t+1 would be the next year.
In this paper, I will develop two linear system models and their corresponding life cycle graphs using the pre-reduction and post-reduction life table data of Uinta Ground Squirrels residing in the edge habitat. I will use the Leslie matrix model to study the age-structured population dynamics of the squirrels.
We will examine the reducibility, primitivity, dominant eigenvalues and their corresponding eigenvectors for each matrix to analyze the long-term dynamics and age distributions of the pre- and post- reduction squirrel populations.
Leslie Matrix Models and Life Cycle Graphs
The simplest model with an age-structure is the Leslie Matrix model. To construct a Leslie matrix, we must establish some rules about the population and the age classes within it. Firstly, we must assume that the population is closed to migration, meaning that no individuals leave the population, and no new individuals enter the population, from the time it is under observation to any time interval it is projected forward onto.
Secondly, only the females of the population are modeled, and this is typically reserved for populations where the number of males can be described in a ratio to the number of females in a population, so we can extrapolate total population insights from the females alone.
Lastly, the time interval coincides with the age interval. To elaborate, let us denote i as the index of an age class in a population, where m is the maximum possible index representing the oldest age class. Under this model, if a squirrel survives the current time interval t and enters the next time interval t+1, they leave their current age class i, and enter the subsequent age class i+1, up until they reach the oldest age class m, where they will remain throughout further time intervals until their death.
Using these rules, it follows that the number of individuals belonging to age class i+1 at time interval t+1 is equal to the number of individuals belonging to the previous age class i at the previous time interval t multiplied by their survival rate, denoted as si. In time interval t+1, the number of individuals in the first age class is equal to the sum of the products of each age class’s population at time interval t and their respective fertility rates, denoted bi.
Using these relationships between the age classes, we can construct equations Xi(t+1) that refer to the number of individuals in an age class i at the subsequent time interval t+1. If we arrange these equations into rows by order of increasing age class, and place the survival rates of each age class under their respective birth rate from the first age group equation such that each term in the equations belongs to a column representing an age class, we see an (m x m) matrix form, where each row corresponds to an age class’s population, and each column corresponds to what that age class contributes to the population of every other age class.
For every age class greater than 1, their population only depends on the survival rate of the previous age class, so the remaining entries in this matrix are zeroes. As we are studying Uinta Ground Squirrels with 3 age classes, we know that m is equal to 3, and the following matrix model is formed, where L refers to the Leslie matrix.
| x1(t + 1) |
| x2(t + 1) |
| x3(t + 1) |
| b1 | b2 | b3 |
| s1 | 0 | 0 |
| 0 | s2 | 0 |
| x1(t ) |
| x2(t ) |
| x3(t ) |
Figure 2: An example of a Leslie matrix for a population with 3 age classes
Let us denote P as the Leslie matrix of the pre-reduction population, and Q as the Leslie matrix of the post-reduction population, with the x functions referring to the number of individuals in an age group n at time periods t and t+1 in both models. Using the data provided in the assignment description, we can construct the following linear system models in matrix form:
Pre-reduction:
| x1(t + 1) |
| x2(t + 1) |
| x3(t + 1) |
| 0.445 | 0.845 | 0.823 |
| 0.350 | 0 | 0 |
| 0 | 0.440 | 0 |
| x1(t ) |
| x2(t ) |
| x3(t ) |
Figure 3: A Leslie matrix for the squirrel population in the edge habitat (before the population reduction)
Post-reduction:
| x1(t + 1) |
| x2(t + 1) |
| x3(t + 1) |
| 0.334 | 1.880 | 0.934 |
| 0.167 | 0 | 0 |
| 0 | 1.000 | 0 |
| x1(t ) |
| x2(t ) |
| x3(t ) |
Figure 4: A Leslie matrix for the squirrel population in the edge habitat (after the population reduction)
Life cycle graphs or directed graphs (digraphs) can be used to represent the relationship between the age groups in a Leslie Matrix. A life cycle graph is composed of nodes and edges, where every age class from 1 to m is represented by its own node, and unidirectional edges connect these nodes, representing what each age class contributes to each other at the subsequent time interval. For the directed graph of a Leslie Matrix, an age class’s node connects to its subsequent age class’s node if the survival rate of the age class is non-zero. Furthermore, every node connects back to the first node which represents the first age class if the fertility rate of the age class represented by that node is non-zero. As a rule of thumb, if any element lij in a Leslie Matrix L is non-zero, an arrow connects the node j to the node i in the digraph.
| x1(t + 1) |
| x2(t + 1) |
| x3(t + 1) |
⋮ |
| xm(t + 1) |
| b1 | b2 | . . . | bm-1 | bm |
| s1 | 0 | . . . | 0 | 0 |
| 0 | s2 | . . . | 0 | 0 |
⋮ | ⋮ | . . . | ⋮ | ⋮ |
| 0 | 0 | . . . | sm-1 | 0 |
| x1(t ) |
| x2(t ) |
| x3(t ) |
⋮ |
| xm(t ) |
Figure 5: A Leslie matrix for a population with m age classes
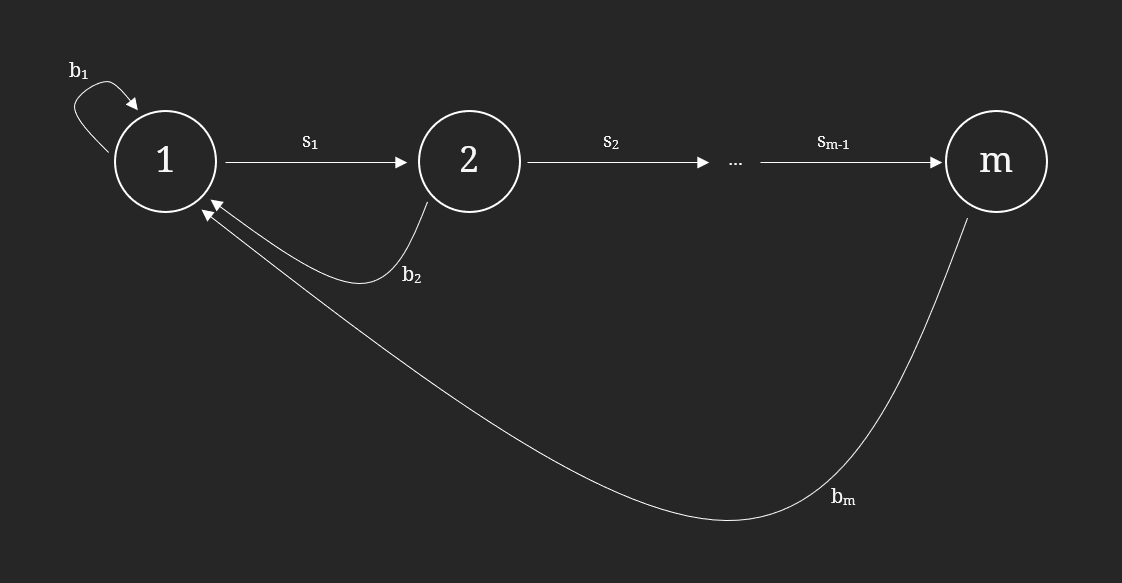
Figure 6: A life cycle graph for a population with m age classes
We can construct the life cycle graphs for the pre-reduction and post-reduction populations of Uinta Ground Squirrels in this form using the provided survival and fertility rates, or using the non-zero elements of their respective Leslie matrices.
Pre-reduction:
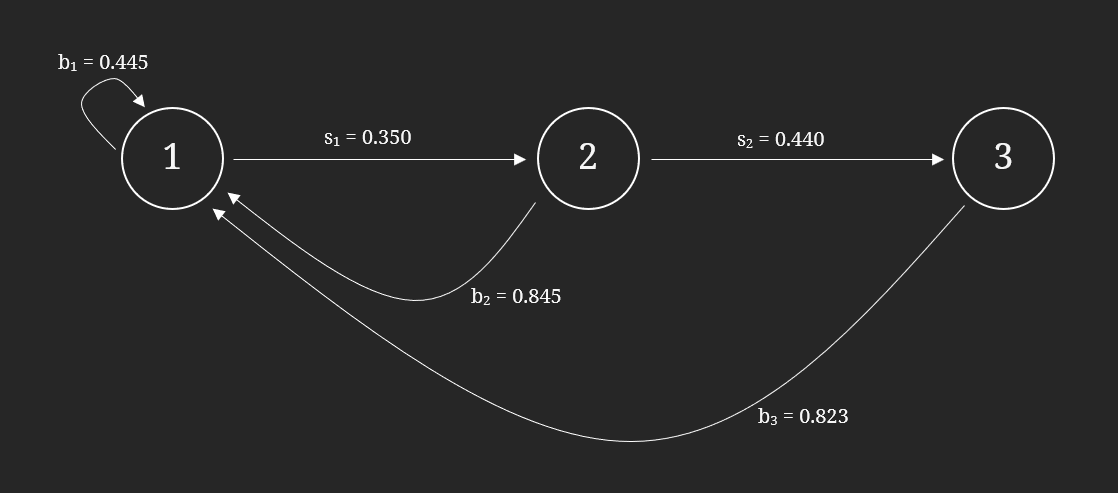
Figure 7: A life cycle graph for the squirrel population before the population reduction
Post-reduction:
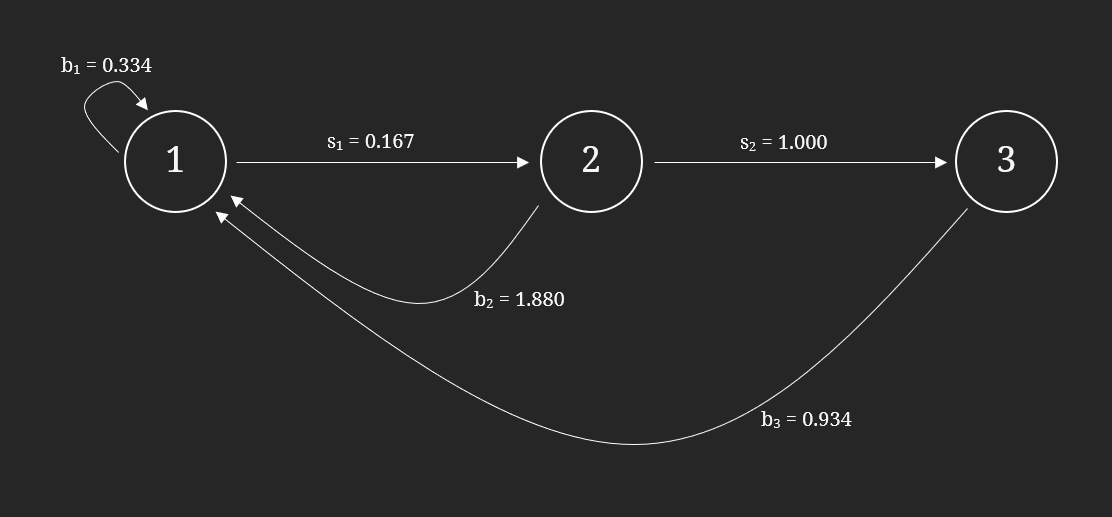
Figure 8: A life cycle graph for the squirrel population after the population reduction
Reducibility, Primitivity, Dominant Eigenvalues, and R0
The matrices of these two systems are irreducible. This is evident as the directed graphs of both pre- and post- reduction populations are strongly connected. In particular, the last element in the first row, which represents the fertility rate of females in the oldest age class, adults, is a non-zero element in both matrices. By definition, the subdiagonal elements of a Leslie matrix are greater than 0, and consequently, are strongly connected. Thus, a requirement for the system described by a Leslie matrix to be irreducible is that its bm, or fertility rate of its oldest age class is greater than 0, connecting the last state variable xm to the first state variable x1. We see that both systems’ adult fertility rates are greater than 0, and their subdiagonal elements are greater than 0, therefore, both systems are strongly connected and irreducible.
To determine primitivity, we can apply Theorem 1.7 which states that an irreducible Leslie matrix L is primitive if the set of numbers containing the indices of its positive birth rates aren’t factors of each other, or in other words, their greatest common divisor is 1. A simple method to determine primitivity in light of this theorem, is checking if b1, the birth rate of the youngest age class, is greater than 0. This element’s index is 1, which means that it doesn’t matter what combination the indices of the positive birth rates are, because the greatest common divisor of 1 and any other set of positive real numbers will always be 1. In both matrices P and Q, we see that their b1 elements are both positive, thereby satisfying the condition outlined in Theorem 1.7, therefore, they are both primitive matrices.
Another way to determine the primitivity of a matrix is by calculating the number of its eigenvalues with maximum modulus, or dominant eigenvalues. If a matrix has a single dominant eigenvalue, it is considered primitive, and if it has more than one dominant eigenvalue, it is considered imprimitive. Additionally, we can determine if a matrix is primitive by finding some positive, real number n such that Ln > 0. This is evident in both matrices P and Q, where n = 3. In other words, if we raise either Leslie matrix to the power of 3, the resulting matrix contains all positive numbers.
The Frobenius Theorem states that an irreducible, nonnegative matrix always has a positive dominant eigenvalue that is a simple root of its characteristic equation. The Perron Theorem states that a positive matrix always has a real, positive dominant eigenvalue that is a simple root of its characteristic equation. As we have determined that both Leslie matrices representing the population dynamics of pre- and post- reduction Uinta Squirrel populations in the edge habitat are irreducible and primitive, the Perron Theorem applies to both matrices, and we can find their dominant eigenvalues by solving for the roots of their respective characteristic polynomials.
To construct the characteristic polynomial of either system, we begin by finding (L – λI) for each matrix, where λI is the identity matrix multiplied by λ, resulting in a matrix with λ entries along its diagonal and zeroes everywhere else. We then calculate the determinant of each matrix, which should result in a cubic polynomial, which makes sense as both matrices have a dimension of 3. To find the determinant of a 3x3 matrix, we take the minor of each of the 9 terms in the matrix (L – λI), which is simply the determinant of the 2x2 matrix created when ignoring the line and column of the element we’re taking the minor of. Using the minors, we can find the cofactors of each element by taking the product of each element’s minor with its respective place sign, which alternates from + to – across rows and columns, starting with + at position l11.
Finally, we can construct the characteristic polynomial by taking the sum of the products of elements in any row or column in (L – λI) with their respective cofactors. I will outline this process by showing both cofactor matrices and their characteristic polynomials.
Pre-reduction
| 0.445 - λ | 0.845 | 0.823 |
| 0.350 | - λ | 0 |
| 0 | 0.440 | - λ |
| λ2 | 0.350λ | 0.154 |
| 0.845λ + 0.362 | λ2 - 0.445λ | 0.440λ - 0.196 |
| 0.823λ | 0.288 | λ2 - 0.445λ - 0.296 |
det(P – λI) = (0 × 0.823λ) + (0.440 × 0.288) + (-λ × (λ2 – 0.445λ – 0.296))
det(P – λI) = -λ3 + (0.445 × λ2) + (0.296 × λ) + 0.128
By Descartes’ rule of signs, this characteristic polynomial has a single change in signs, meaning this polynomial has a single positive root. That positive root will be our dominant eigenvalue.
When we solve this characteristic polynomial, where a = -1, b = 0.445, c = 0.296, and d = 0.128, there are 3 roots. Two of these solutions are a pair of complex conjugates, x1 = -0.237 + 0.288i and x2 = -0.237 - 0.288i.
The last solution is a positive real number, x3 = 0.918. We can conclude that 0.918 is the dominant eigenvalue as it is greater in magnitude than both complex conjugates, which have the same magnitude of √
(-0.237)2+0.2882.
Since the dominant eigenvalue is less than 1, we can conclude that R0, the inherent net reproductive number, which refers to the number of offspring that an individual has in their lifetime, is also less than one. We can also calculate this in the following equation:
R0 = b1 + b2s1 + b3s1s2
R0 = 0.445 + (0.845 × 0.350) + (0.823 × 0.350 × 0.440) = 0.868
Both R0 and λ1 are less than 1, which means that this population eventually goes extinct, after enough time, given there are no changes in the state of this system.
Post-reduction
| 0.334 - λ | 1.880 | 0.934 |
| 0.167 | - λ | 0 |
| 0 | 1.000 | - λ |
| λ2 | 0.167λ | 0.167 |
| 1.880λ + 0.934 | λ2 - 0.334λ | λ - 0.334 |
| 0.934λ | 0.156 | λ2 - 0.334λ - 0.314 |
det(Q – λI) = (0 × 0.934λ) + (1.000 × 0.156) + (-λ × (λ2 – 0.334λ – 0.314))
det(Q – λI) = -λ3 + (0.334 × λ2) + (0.314 × λ) + 0.156
By Descartes’ rule of signs, this characteristic polynomial has a single change in signs, meaning this polynomial has a single positive root. That positive root will be our dominant eigenvalue.
When we solve this characteristic polynomial, where a = -1, b = 0.334, c = 0.314, and d = 0.156, there are 3 roots. Two of these solutions are a pair of complex conjugates with the same absolute value, x1 = -0.276 + 0.316i and x2 = -0.276 - 0.316i.
The last solution is a positive real number, x3 = 0.887. We can conclude that 0.887 is the dominant eigenvalue as it is greater in magnitude than both complex conjugates, which have the same magnitude of √
(-0.276)2+0.3162.
Since the dominant eigenvalue is less than 1, we can conclude that R0, the inherent net reproductive number, which refers to the number of offspring that an individual has in their lifetime, is also less than one. We can also calculate this in the following equation:
R0 = b1 + b2s1 + b3s1s2
R0 = 0.334 + (1.880 × 0.167) + (0.934 × 0.167 × 1.000) = 0.804
Both R0 and λ1 are less than 1, which means that this population eventually goes extinct, after enough time, given there are no changes in the state of this system.
Comparing both systems’ dominant eigenvalues and inherent net reproductive numbers, we can see that the post-reduction population’s values have decreased slightly across the board, meaning the long-term outcomes of the edge population have worsened as a result of this population density reduction. Interestingly enough, the dominant eigenvalues and inherent net reproductive numbers of lawn and non-lawn populations have increased dramatically after their population density reductions.
This presents an interesting case study, as it raises some important questions. Namely, what is it about an edge habitat, which is a transitory space between two defined habitats, which results in such different outcomes compared to the lawn and non-lawn habitats? Lawn habitats are typically lower in biodiversity when it comes to other animals, as well as the flora and fauna in the ecosystem, compared to non-lawn habitats. I would imagine that the edge habitat between these two types has aspects of both in varying gradients across the landscape, but I don’t understand why a mixture of both habitats would result in such different outcomes compared to the individual habitats themselves.
Another interesting observation – the survival rate of yearlings after this reduction in the edge environment is 100%, which means that every single yearling survives the year it takes to become an adult. Not only that, but their fertility rate increased the most dramatically, and ended up being the highest fertility rate across age classes and habitats.
This raises another important question, why has the inherent net reproductive number for the edge habitat squirrels decreased when their yearling survival and fertility rates have exploded to astronomical amounts? This is intriguing, especially because the fertility and survival rates of adults and young remained relatively consistent across the reduction, except for the survival rate of young after the reduction. We see that this rate has halved as a result of the reduction, possibly because there are less squirrels to take care of their young in this habitat, where there are potentially more predators and variables at play which put these vulnerable segments of the population at risk.
In any case, the affect of this halved survival rate is evident when we look at the relationship it has with the inherent net reproductive number. We see that every term used to calculate R0 is multiplied by s1. Since s1 was effectively halved, so was R0, however this effect was cancelled out by the dramatic increase in survival and fertility rates of yearlings, but not quite, which is why we see a slight decrease overall. This serves as an important reminder, that the survival rate of the youngest age class of a population has far-reaching affects, as every other population segment depends on its previous age segments surviving and reproducing to exist.
Population Age Distributions
To see how the distribution of age segments in a population change over time, we must first calculate the stable age distribution, which is the eigenvector which corresponds to the dominant eigenvalue of a Leslie matrix. This vector is used to calculate future distributions as it is associated with the dominant eigenvalue, which defines the population number. As the dominant eigenvector, it makes sense that the dominant eigenvalues multiplied by this vector are also what define the segments in each population, over smaller eigenvectors.
To find our stable age distribution, or v1 which corresponds to λ1, we calculate (L – λ1I), which is the Leslie matrix subtracting the dominant eigenvalue for each term in its diagonal. We then multiply this with the vector v1 and set it to 0 to solve for v11, v12, and v13 in a system of equations.
To project the population age distributions forward in time, we multiply the Leslie matrix by this stable age distribution. To project forward n years, we raise the power of the Leslie matrix by n, and multiply it with the stable age distribution to get the age distribution at time period n.
Pre-reduction
| 0.445 - 0.918 | 0.845 | 0.823 |
| 0.350 | -0.918 | 0 |
| 0 | 0.440 | -0.918 |
| -0.473 | 0.845 | 0.823 |
| 0.350 | -0.918 | 0 |
| 0 | 0.440 | -0.918 |
| -0.473 | 0.845 | 0.823 |
| 0.350 | -0.918 | 0 |
| 0 | 0.440 | -0.918 |
(-0.473 × v11) + (0.845 × v12) + (0.823 × v13) = 0
(0.350 × v11) – (0.918 × v12) = 0
(0.440 × v12) – (0.918 × v13) = 0
Solving this system of linear equations we find that
| 1 |
| 0.381 |
| 0.183 |
By arbitrarily setting v11 to 1. Normalizing this vector, we find that
| 0.639 |
| 0.244 |
| 0.117 |
I want to compare the age distribution after 1 year, 5 years, and 10 years, so we will compute P5 and P10 and multiply those matrices with v1 to find those vectors.
| 0.389 | 0.524 | 0.342 |
| 0.145 | 0.204 | 0.138 |
| 0.074 | 0.089 | 0.063 |
| 0.252 | 0.341 | 0.226 |
| 0.096 | 0.130 | 0.086 |
| 0.046 | 0.062 | 0.041 |
Post-reduction
| 0.334 - 0.887 | 1.880 | 0.934 |
| 0.167 | -0.887 | 0 |
| 0 | 1.000 | -0.887 |
| -0.553 | 1.880 | 0.934 |
| 0.167 | -0.887 | 0 |
| 0 | 1.000 | -0.887 |
| -0.553 | 1.880 | 0.934 |
| 0.167 | -0.887 | 0 |
| 0 | 1.000 | -0.887 |
(-0.553 × v11) + (1.880 × v12) + (0.934 × v13) = 0
(0.167 × v11) – (0.887 × v12) = 0
(1.000 × v12 – (0.887 × v13) = 0
Solving this system of linear equations, we find that
| 1 |
| 4.705 |
| 4.173 |
By arbitrarily setting v11 to 1. Normalizing this vector, we find that
| 0.101 |
| 0.422 |
| 0.476 |
Next, we compute Q5 and Q10 and multiply those matrices with v1 to find those vectors.
| 0.300 | 0.978 | 0.299 |
| 0.053 | 0.193 | 0.063 |
| 0.067 | 0.186 | 0.066 |
| 0.162 | 0.538 | 0.171 |
| 0.031 | 0.101 | 0.032 |
| 0.035 | 0.114 | 0.036 |
The results of the age distribution projections are summarized in the table below:
| Population Type | Stable Age Distribution (v1) | t = 1 | t = 5 | t = 10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pre-reduction | (
) | (
) | (
) | (
) | ||||||||||||
| Post-reduction | (
) | (
) | (
) | (
) |
Figure 9: Age distribution table for the population - each column corresponds to the proportion of an age-segment (young, yearling, adult) to the total population
We can see that the age distribution for the pre-reduction remains stable throughout 10 years after the time of the experiment. For the post-reduction population, we see a stark difference in the stable age distribution, and that is outlined in the trend we see emerge as the years progress, among the three age classes. The distribution of young decreases and the distribution of yearlings and adults increase in lockstep to compensate. Furthermore, the rate at which this decrease occurs slows down, as we can see the distribution of young at t = 1 compared to t = 5 decreases faster than the distribution of young at t = 5 to t = 10.
Additionally, we observe that the proportion of adults increases more than the proportion of yearlings, which is reflected both in the post-reduction population’s stable age distribution, which guarantees that future age distribution will be a multiple of this vector, but it is also outlined in the life table of the population. The survival rate of young is effectively halved after the reduction, which drastically impacts the number of yearlings which exist in the following years. As for the yearlings that do survive, perhaps because of decreased competition, they thrive as all of them survive to adulthood, and their fertility rates indicate that they contribute heavily towards following years’ young population.
References
Allen, L. J. S. (2007). An introduction to mathematical biology. Pearson/Prentice Hall.
Oli, M. K., Slade, N. A., & Dobson, F. S. (2001). Effect of density reduction on Uinta Ground Squirrels: Analysis of Life Table Response Experiments. Ecology, 82(7), 1921–1929.